Introduction to Dynamic Programming
Introduction to Dynamic Programming
What’s Dynamic Programming?
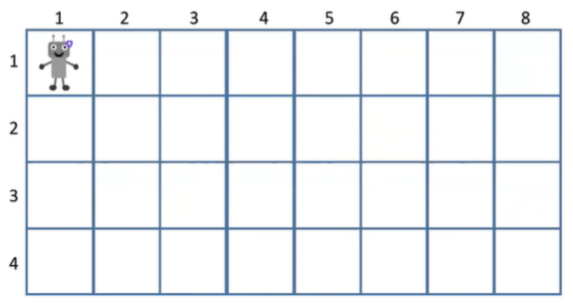
给定一个矩阵网络,一个机器人从左上角出发,每次可以向下或向右走一步
题A:求有多少种方式走到右下角
题B:输出所有走到右下角的路径
动态规划题目特点
- 计数
- 有多少种方式走到右下角
- 有多少种方法选出 k 个数使得和是 Sum
- 求最大最小值
- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度
- 求存在性
- 取石子儿游戏,先手是否必胜
- 能不能取出 k 个数使得和是 Sum
Coin Change
你有三种硬币,分别面值2元,5元和7元,每种硬币都有足够多,买一本书需要27元。
如何用最少的硬币组合正好付清,不需要对方找钱
(求最大最小值类型的动态规划)
来自大脑直觉的思路
- 改算法:尽量用大的硬币,最后如果可以用一种硬币付清就行
- 7 + 7 + 7 = 21
- 21 + 2 + 2 + = 27
- 6枚硬币,应该对了吧。。。
然鹅,正确答案是:7 + 5 + 5 + 5 + 5 = 27,五枚硬币
动态规划组成部分一:确定状态
- 状态在动态规划中的作用属于定海神针
- 简单的说,解动态规划的时候需要开一个数组,数组的每个元素
f[i]或者f[i][j]代表什么?- 类似于解数学题中,X,Y,Z 代表什么
确定状态需要两个意识:
最后一步
子问题
最后一步
虽然我们不知道最优策略是什么,但是最优策略肯定是K枚硬币 a1, a2, …, ak 面值加起来是27
所以一定有一枚最后的硬币:ak
除掉这枚硬币,前面硬币的面值加起来是27 - ak
- 关键点1:我们不关心前面的k-1枚硬币是怎么拼出 27-ak 的(可能有1种拼法,可能有100种拼法),而且我们现在甚至还不知道ak和K,但是我们确定前面的硬币拼出了27-ak
- 关键点2:因为是最优策略,所以拼出27-ak的硬币数一定要最少,否则这就不是最优策略了
- 所以我们就要求:最少用多少枚硬币可以拼出27-ak
- 原问题是最少用多少枚硬币拼出27
- 我们将原问题转化成了一个子问题,而且规模更小:27-ak
子问题
所以我们就要求:最少用多少枚硬币可以拼出27-ak
原问题是最少用多少枚硬币拼出27
我们将原问题转化成了一个子问题,而且规模更小:27-ak
为了简化定义,我们设状态 f(x)= 最少用多少枚硬币拼出X
等等,我们还不知道最后那枚硬币 ak 是多少
最后那枚硬币 ak 只可能是 2, 5 或者 7
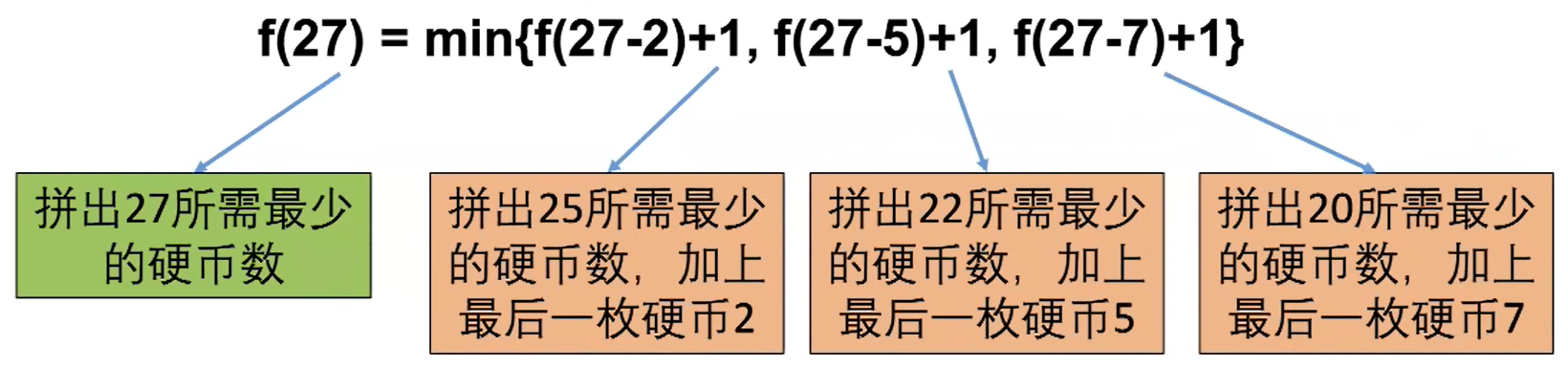
如果 ak 是2,f(27) 应该是 f(27-2) + 1 (加上最后这一枚硬币2)
如果 ak 是5,f(27) 应该是 f(27-5) + 1 (加上最后这一枚硬币5)
如果 ak 是7,f(27) 应该是 f(27-7) + 1 (加上最后这一枚硬币7)
除此以外,没有其他的可能了
需要求最少的硬币数,所以:
f(27) = min{ f(27-2)+1, f(27-5)+1, f(27-7)+1 }
递归解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int f(int X) { // f(X)= 最少用多少枚硬币拼出X
if (X == 0) return 0; // 0 元钱只要 0 枚硬币
int res = MAX_VALUE; // 初始化用无穷大
if (X >= 2) { // 最后一枚硬币是 2 元
res = Math.min(f(X-2)+1, res);
}
if (X >= 5) { // 最后一枚硬币是 5 元
res = Math.min(f(X-5)+1, res);
}
if (X >= 7) { // 最后一枚硬币是 7 元
res = Math.min(f(X-7)+1, res);
}
return res;
}
思考:为什么初始化的时候用了无穷大呢?
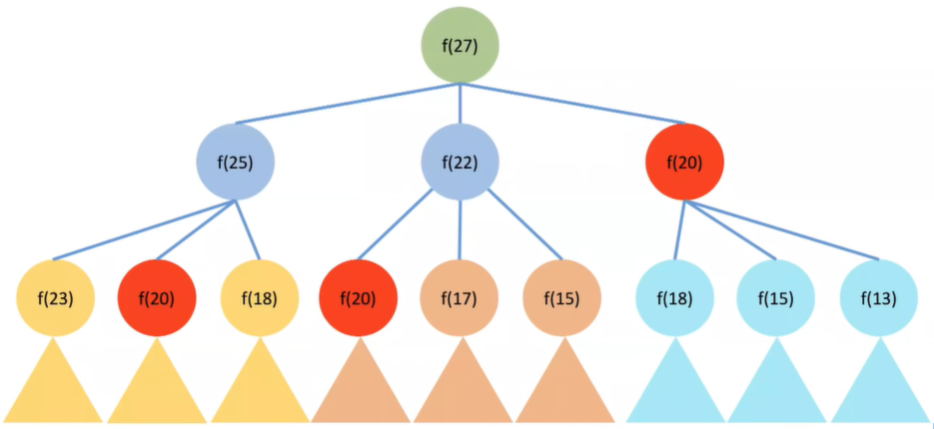
递归解法的问题
- 做了很多重复计算,效率低下
- 如何避免?-> 将计算结果保存下来,并改变计算顺序
动态规划组成部分二:转移方程
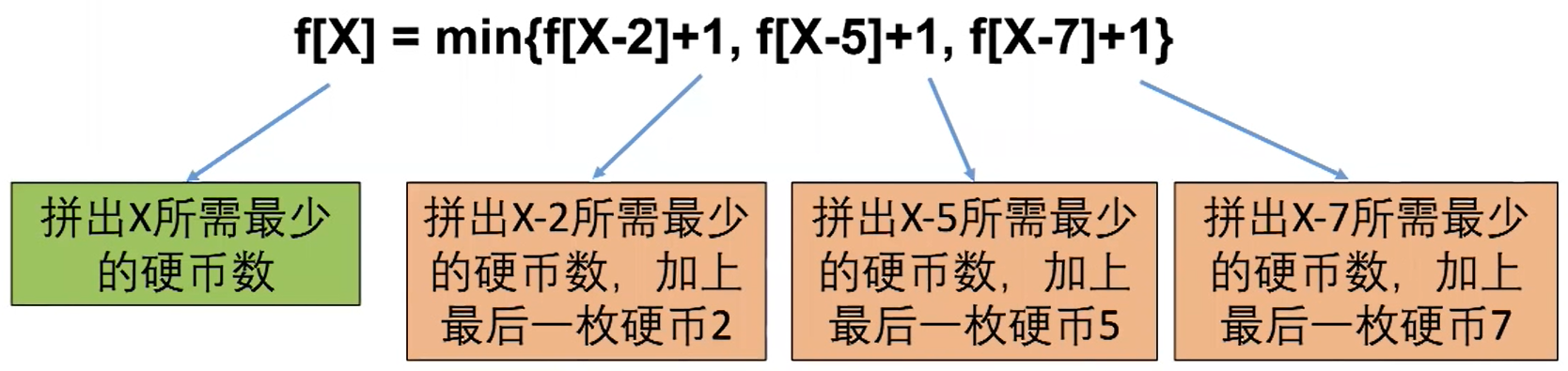
设状态 f[X]= 最少用多少枚硬币拼出X
动态规划组成部分三:初始条件和边界情况
f[x] = min{ f[X-2]+1, f[X-5]+1, f[X-7]+1 }
两个问题:X-2, X-5 或者 X-7 小于 0 怎么办?什么时候停下来?
如果不能拼出Y,就定义 f[Y]= 正无穷;例如f[-1] = f[-2] = … = 正无穷
(用转移方程计算不出来的,就需要手工定义)
所以f[1]=min{f[-1]+1, f[-4]+1, f[-6]+1 } = 正无穷,表示拼不出来1
初始条件:f[0] = 0
动态规划组成部分四:计算顺序
拼出 X 所需要的最少硬币数:f[X] = min{ f[X-2]+1, f[X-5]+1, f[X-7]+1 }
初始条件:f[0]=0
然后计算 f[1], f[2], … , f[27]
当我们计算到 f[X] 时,f[X-2],f[X-5],f[X-7] 都已经得到结果了
f[X] = 最少用多少枚硬币拼出X
f[X] = 正无穷 表示无法用硬币拼出X
- 每一步尝试三种硬币,一共27步
- 与递归算法相比,没有任何重复计算
- 算法时间复杂度(即需要进行的步数)273 (nm)
- 递归时间复杂度:»27*3
小结
求最值型动态规划
动态规划组成部分
确定状态
最后一步(最优策略中使用的最后一枚硬币a)
化成子问题(最少的硬币拼出更小的面值27-a)
- 转移方程
- f[X]=min{f[X-2]+1, f[X-5]+1, f[X-7]+1 }
- 初始条件和边界情况
- f[0] = 0,如果不能拼出Y,f[Y] = 正无穷
- 计算顺序
- f[0], f[1], f[2], …
消除冗余,加速计算
现场写代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public calss Solution {
// int[] coins, int amount
// A { 2, 5, 7 } M 27
public int coinChange(int[] A, int M) {
// 0 ... n : [n+1]
// 0 ... n-a : [n]
int[] f = new int[M + 1];
int n = A.length; // number of kinds of coins
// initialization
f[0] = 0;
int i, j;
// f[1], f[2], ..., f[27]
for (i = 1; i <= M; ++i) {
f[i] = Integer.MAX_VALUE;
// last coin A[j]
// f[i] = min{f[i-A[0]]+1, ... , f[i-A[n-1]]+1}
for (j = 0; j < n; ++j) {
if (i >= A[j] && f[i - A[j]] != Integer.MAX_VALUE) {
f[i] = Math.min(f[i - A[j]] + 1, f[i]);
}
}
}
// cannot be made up by any combination of the coins
// return -1
if (f[M] == Integer.MAX_VALUE) {
f[M] = -1;
}
return f[M];
}
}
- 开辟空间大小对不对?-> int[] f = new int[M + 1];
- 初始化了吗? -> f[0] = 0;
- 顺序对不对 -> for (i = 1; i <= M; ++i)
- 你怎么去处理f[i] -> f[i] = Integer.MAX_VALUE;
- 你的状态转移方程有没有写对呢? -> f[i] = Math.min(f[i - A[j]] + 1, f[i]);
Unique Paths
Description
Lintcode https://www.lintcode.com/problem/unique-paths/
Leetcode https://leetcode.com/problems/unique-paths/
Solution https://www.jiuzhang.com/solutions/unique-paths/
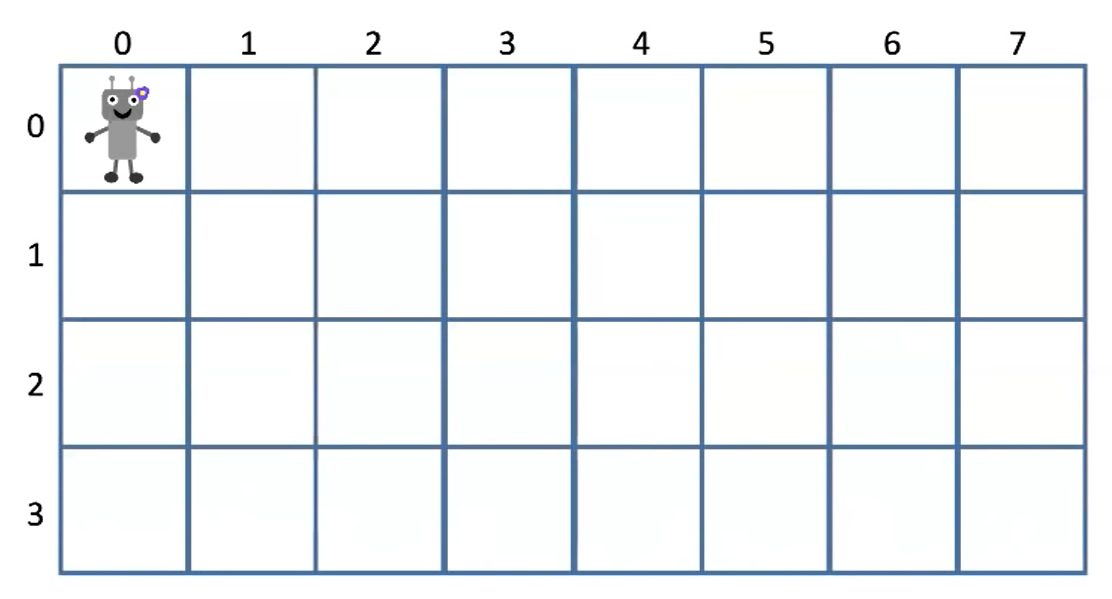
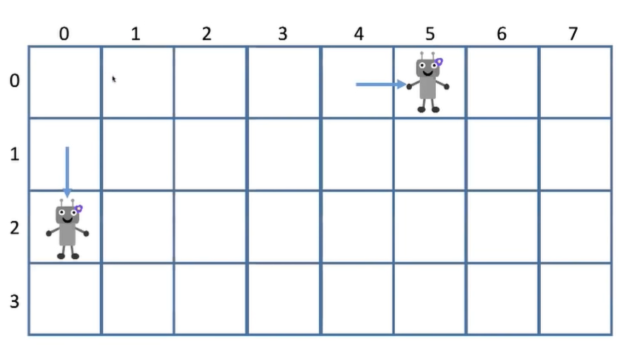
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.
Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
The test cases are generated so that the answer will be less than or equal to 2 * 10^9.
题意:
给定m行n列的网格,有一个机器人从左上角(0,0出发,每一步可以向下
或者向右走一步
问有多少种不同的方式走到右下角
(计数型动态规划)
四个组成部分,好就好在不管是什么样的动态规划都要用这四部分!!!
确定状态
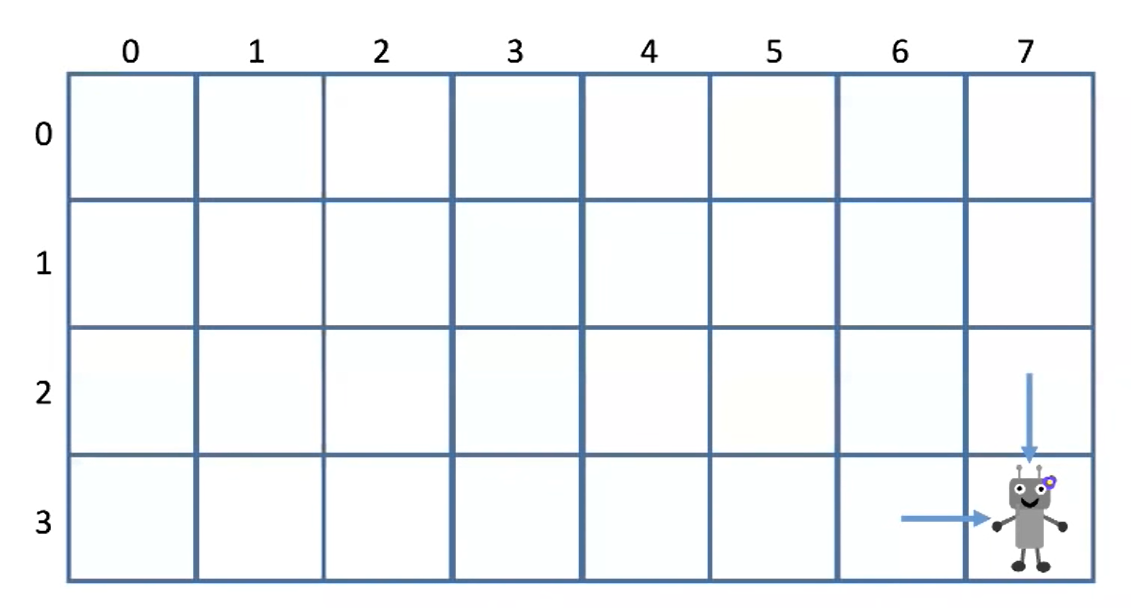
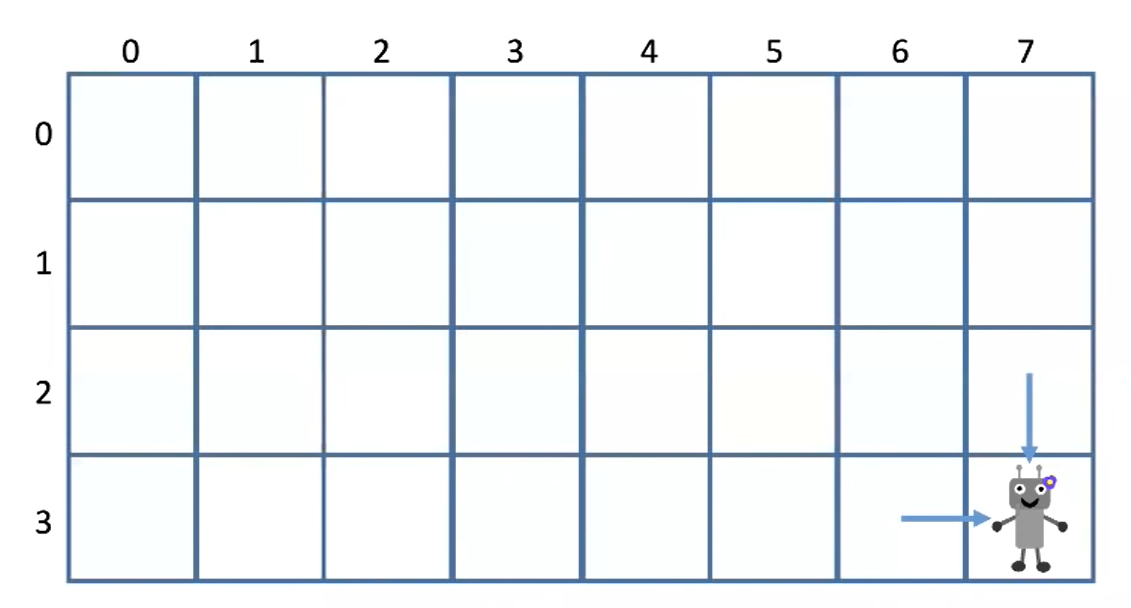
最后一步:无论机器人用何种方式到达右下角,总有最后挪动的一步:
向右或者向下
右下角坐标设为(m-1,n-1)
那么前一步机器人一定是在 (m-2, n-1) 或者 (m-1, n-2)
加法原理:1 无重复 2 无遗漏
加法原理是一个基本的数学原理,它用于计算两个或多个事件的总数,前提是这些事件是互相独立的,即一个事件的发生不影响其他事件的发生。简而言之,加法原理规定,如果有两个事件A和B,那么它们同时发生的总数等于事件A发生的总数加上事件B发生的总数。
数学表达方式如下:
如果事件A有n种可能发生的方式,事件B有m种可能发生的方式,那么事件A和事件B同时发生的总数为n + m。
这个原理可以扩展到更多的事件。例如,如果有三个事件A、B和C,且它们都是互相独立的,那么它们同时发生的总数为n + m + p,其中n是事件A的可能方式数,m是事件B的可能方式数,p是事件C的可能方式数。
加法原理的数学表达式如下:
如果事件A有n种可能发生的方式,事件B有m种可能发生的方式,那么事件A和事件B同时发生的总数为:
n + m
这个公式可以扩展到更多的事件,比如有三个事件A、B和C,那么它们同时发生的总数为:
n + m + p
其中n是事件A的可能方式数,m是事件B的可能方式数,p是事件C的可能方式数,依此类推。这个公式描述了互相独立事件的总数计算方法。
如果有两个变量就开辟一个二维数组,如果只有一个变量就开辟一维数组
那么,如果机器人有X种方式从左上角走到 (m-2, n-1),有 Y 种方式从左上角走到(m-1, n-2),则机器人有X+Y种方式走到 (m-1, n-1)
思考:为什么是x+y
问题转化为,机器人有多少种方式从左上角走到 (m-2, n-1) 和(m-1, n-2)
原题要求有多少种方式从左上角走到 (m-1, n-1)
那么就有了子问题
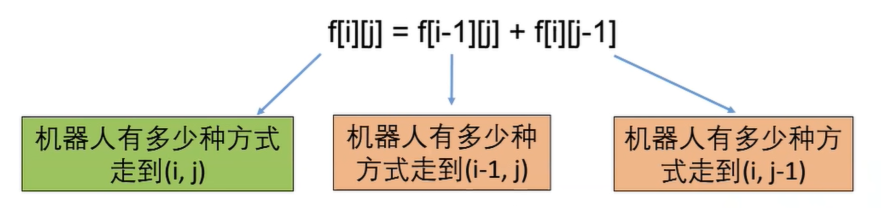
状态:设 f[i][j] 为机器人有多少种方式从左上角走到 (i, j)
转移方程
- 对于任意一个格子 (i, j)
初始条件和边界情况
- 初始条件:f[0][0] = 1,因为机器人只有一种方式到左上角
- 边界情况:i=0 或 j=0,则前一步只能有一个方向过来 -> f[i][j]=1
计算顺序
- f[0][0] = 1
- 计算第 0 行:f[0][0], f[0][1], … , f[0][n-1]
- 计算第 1 行:f[0][1], f[1][1], … , f[1][n-1]
- …
- 计算第 m-1 行:f[m-1][0], f[m-1][1], … , f[m-1][n-1]
- 答案是 f[m-1][n-1]
- 间复杂度(计算步数):O(MN),空间复杂度(数组大小): O(MN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
public int uniquePaths(int m, int n) {
int[][] f = new int[m][n];
int i, j;
for (i = 0; j < n; ++i) { // row: top to bottom
for (j = 0; j < n; ++j) {
if (i == 0 || j == 0) {
f[i][j] = 1;
}
else {
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
} // for j
} // for i
return f[m - 1][n - 1];
}
}
Jump Game
Lintcode https://www.lintcode.com/problem/jump-game/
Leetcode https://leetcode.com/problems/jump-game/
Solution https://www.jiuzhang.com/solutions/jump-game/
You are given an integer array nums. You are initially positioned at the array’s first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.
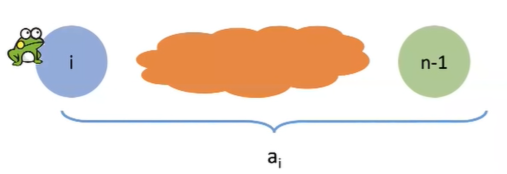
- 有n块石头分别在x轴的 0, 1, … , n-1 位置
- 一只青蛙在石头 0,想跳到石头 n-1
- 如果青蛙在第块石头上,它最多可以向右跳距离ai
- 问青蛙能否跳到石头n-1
- 例子:
- 输入:a=[2, 3, 1, 1, 4]
- 输出:True
- 输入:a=[3, 2, 1, 0, 4]
- 输出:False
(存在型动态规划)
输出 True 和 False 一看就是存在型的动态规划!!!
确定状态
最后一步:如果青蛙能跳到最后一块石头n-1,我们考虑它跳的最后一步
这一步是从石头跳过来,i<n-1
这需要两个条件同时满足:
青蛙可以跳到石头i
最后一步不超过跳跃的最大距离:n-1-i < ai
子问题
那么,我们需要知道青蛙能不能跳到石头i(i<n-1)
而我们原来要求青蛙能不能跳到石头n-1
那么就出现了子问题
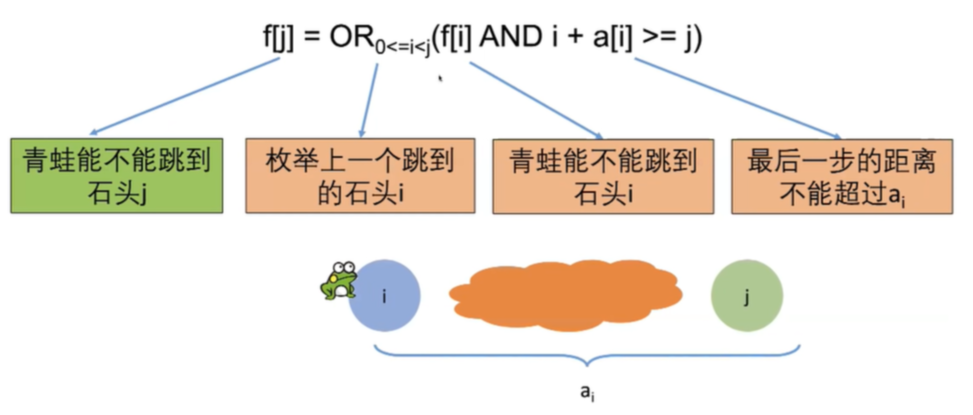
状态:设f[j]表示青蛙能不能跳到石头
转移方程
设 f[j] 表示青蛙能不能跳到石头j
计算顺序
设 f[j] 表示青蛙能不能跳到石头
f[j] = OR(f[i] AND i+a[i]>=j) 范围是0<=i<j 初始化f[0]=True
计算f[1], f[2], … , f[n-1]
答案是f[n-1]
时间复杂度:O(N^2),空间复杂度(数组大小):O(N)
Solutions
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class Solution {
public boolean canJump(int[] A) {
int n = A.length;
boolean[] f = new boolean[n];
f[0] = true; // initialization
for (int j = 1; j < n; ++j) {
f[j] = false;
// previous stone i
// last jump is from i to j
for (int i = 0; i < j; ++i) {
if (f[i] && i + A[i] >= j) {
f[j] = true;
break;
}
} // for i
} // for j
return f[n - 1];
}
}
Notice
This problem have two method which is Greedy and Dynamic Programming.
The time complexity of Greedy method is O(n).
The time complexity of Dynamic Programming method is O(n^2).
We manually set the small data set to allow you pass the test in both ways. This is just to let you learn how to use this problem in dynamic programming ways. If you finish it in dynamic programming ways, you can try greedy method to make it.
Homework: Maximum Product Subarray
Leetcode https://leetcode.cn/problems/maximum-product-subarray/
Solution https://www.jiuzhang.com/solutions/maximum-product-subarray
Conclusion - Introduction to DP
四个组成部分
- 确定状态
- 研究最优策略的最后一步
- 化为子问题
- 转移方程
- 根据子问题定义直接得到
- 初始条件和边界情况
- 细心,考虑周全
- 计算顺序
- 利用之前的计算结果